さあ。今日からいよいよ分数のお勉強です。
子供も、それを楽しみにしています。その様子を見てみましょう:
母と子のお勉強 その1
母「 ![]() を“5ぶんの1”って言うの。こういう数を“分数”って言うのよ。
を“5ぶんの1”って言うの。こういう数を“分数”って言うのよ。
下にあるほうの数を分母って言うの。上にある数は分子って言うのよ。ホラ、お母さんが子供をオンブしているみたいでしょ?」
子「ホントだ。おもしろーい。」
母「じゃあ、書く練習をしてみようね。まず、棒をはじめに真ん中に書いて」(書いてみせる)
母「書いてごらん。」
子「こう?」(子供が自分のノートに書く。)
母「そうそう。上手ね。次は分母よ。先にお母さんが立ってないとオンブできないわね。」(棒の下に5と書く。)
母「書いてごらん。」
子「こう?」(子供が自分のノートに書く。)
母「そうそう。上手。そして、分子よ。」(棒の上に1と書く。)
母「書いてごらん。」
子「赤ちゃんだね。」(子供が自分のノートに書く。)
母「上手に書けたわね。 じゃあ、“5ぶんの1”って言いながら、3回書いてみようか。」
子「5ぶんの1」(子供が自分のノートに書く。)
子「5ぶんの1」(子供が自分のノートに書く。)
子「5ぶんの1」(子供が自分のノートに書く。)
母「すごく上手よ。さあ。それじゃあ、分数の足し算を教えてあげるわね。」
母「 ![]() という足し算よ。これはね、分母の5はそのままで、分子だけを足すの。だから、答は
という足し算よ。これはね、分母の5はそのままで、分子だけを足すの。だから、答は ![]() よ。」
よ。」
母「じゃあ、これはどうなるか分かるかな? ![]() は?」
は?」
子「えーっと。5はそのままで、ん〜っと。わかった。 ![]() だ。」
だ。」
母「はい。よくできました。そういうこと。じゃ、他にもいっぱい練習してみようね。」
と言って、練習用のプリントに入る。
.
そして、足し算も、やり方をきちんと説明した後、数字を変えて別の問題を考えさせて慣れさせ、それから数を増やして練習に入る。そこまでの流れです。段階的で、無理なく子供は上って行けます。
ただ、大変大切な事が一つ抜けているのです。
それは何でしょうか?
2点、あります:
第1点めは、新しく出てきた「分数」という概念を、まず体感させる、ということです。
数学的対象は、学習する内容が高度になるほど次第に抽象的なものになっていきますが、分数は身の回りにもいろいろと出てくるものです。
できるだけ、そのような身の回りの「分数」との出会いを持ちましょう。
それまでの体験が豊富であれば、絵を描いて説明すれば、十分に分かるでしょう。もし、ピンと来ないようであれば、改めてここで手を動かして実物に触れることができるようにしましょう。
たとえば、
母「○○チャンのお誕生日にお母さんがケーキを買ってきたの。さあ。お父さんとお母さんと○○ちゃんとおじいちゃんとおばあちゃんで、みんなおんなじ大きさになるように分けようね。」
と言いながら、ケーキを真上から見た丸を描いて、それを5等分する線を引きます(フリーハンドでさっと描いていきましょう)。
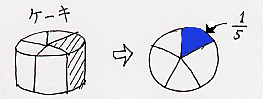
もしも、これまでに、そういう経験がないと、子供にとってはピンと来ないかも知れません。このような体験を、小さいときから十分にさせておくことが大切です。
ここで、”5等分”という言葉を教えておくと、後の説明もしやすくなります。
または、直方体のケーキで説明するのもいいでしょう。子供がようかんを好きなら(子供はあまり甘すぎるお菓子は好きでないかもしれません)、それで説明してもかまいません。ケーキは丸い絵で使ったから、ケーキとは別のものの方がいいです。
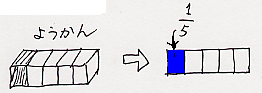
あるいは、長目のテープを5人で分ける、という設定で説明するのもいいですね。
5等分するという図を描くのは少し難しいかもしれません。2等分や4等分の方が子供も描きやすいでしょう。親がいろんな等分の図をかいてやるといいのです。
そして、何分のいくつかを子供に言わせるといいでしょう。リズミカルに進めていくことです。
絵を描いて、「ケーキが1個あるよ。2等分したの。」斜線を引いて「これ何分のいくつかな?」と訊いて、子供に何分のいくつかを言わせていましょう。
子供がすぐ答えられないようなら、にこやかに答を言ってあげればよろしい。
ここは、訓練です。絵を見て何分のいくつかがすぐに言えるようになるまで、繰り返しましょう。
![]() 、
、![]() 、
、![]() 、
、![]() 、 …
、 …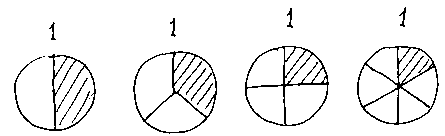
![]() 、
、![]() 、
、![]() 、
、![]() 、 …
、 … 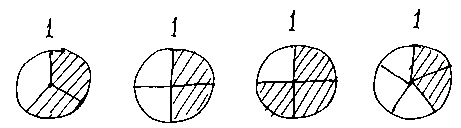
などなど。
こうして、子供は分数という新しい数学的概念を、実態を持った数として、吸収するのです。
ここで、いろいろな分数を見せるとき、その分数が何分のいくつかをいえたら、同時に、ケーキ全体は1であることを押さえておきましょう。
小さなケーキ、大きなケーキ、丸いケーキ、四角いケーキ…、いろんなケーキを描きながら、
「全体は1、それを何等分したうちのいくつ分が、何分のいくつ。」
と、分数と結びつけることを繰り返しながら、子供は分数というものが、割合を表しているんだということをも潜在的につかんでいきます。
このように身の回りのいろんなところに、「分数」が存在しているんだということを、手で触って動かして納得すること。
新しい概念が出てきたときにはこれをしっかりやることが必要です。
※ ※ ※
第2点めは、足し算をそのようにする理由を納得させる、ということです。
上のお母さんの指導には、それが抜けています。説明のしかたはていねいでわかりやすいのですが、ただやり方を説明しただけであって、どうして分子だけを足すのかその説明がありません。
このような教え方が一概に悪いと言うのではありません。特に子供がとても小さいときは柔軟ですから、スピーディに(1秒に1枚)フラッシュさせながら、大量のカードを見せて、分数の足し算を教え込む方法があります。(これは別のところで紹介します。)子供の中の処理を右脳につなぐのです。
ただし、子供が3歳を過ぎると、「どうして?」という理由を子ども自身が追究するようになります。論理的思考の芽生えです。数学においては、論理的思考がその中心です。これは左脳で処理します。
この、「左脳へのつなぎ」が、「理由を納得する」ということなのです。
つまり、どのように導入していくにせよ、その指導の中に、
「なぜ、そうするのか?」
という理由の確認を必ず入れるようにしましょう。
上のように教えたとき、子供がもしも、納得せずに
「えっ?お母さん、どうして? どうして、上(分子)だけ足すの? どうして下(分母)は足さないの?」
と聞いてくるなら、チャンスです。また、そのような追求ができる子供は、数学的に伸びていきます。
理由なしに足し算のルールを決めるのなら、
![]()
でも、理にかなっていると言えます。
どうして、そうならないのか、子供が疑問に持つならば、それが論理的な追究心の芽生えです。そこを大切にしましょう。
もし、子供が何の疑問も持たないならば、逆にこちらから問いかけて、揺さぶってあげるといいでしょう。
この理由の説明は、最初に分数が出てきたとき、身の回りのケーキなどで十分に実態的につかむ作業をやっていれば、簡単ですね。
母「おじいちゃんとおばあちゃんのケーキを合わせると![]() 個だね。やさしい○○ちゃんは、『ボクのもあげるよ』と言って、自分のケーキをおじいちゃんとおばあちゃんにあげました。さて、おじいちゃんとおばあちゃんのケーキは全部で何分のいくつになったかな?」
個だね。やさしい○○ちゃんは、『ボクのもあげるよ』と言って、自分のケーキをおじいちゃんとおばあちゃんにあげました。さて、おじいちゃんとおばあちゃんのケーキは全部で何分のいくつになったかな?」
たとえば、こんな風に説明できますね。
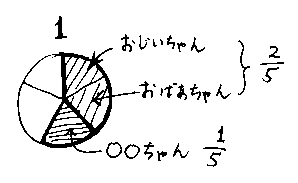
分数の実態を把握している子供たちは、![]() だということを、納得します。
だということを、納得します。
以上のように、
数学的概念の実態をつかみ、納得する
という作業を、数学教育アカデミーでは、大切にします。
これが、数学教育アカデミーが《スーパーらくらくスタディ》で提唱する「情知意サイクル」の「情」なのです。
。。。。。。。。。。。。。。。。