さあ。今日からいよいよ分数の約分のお勉強です。
今日も子供は、それを楽しみにしています。その様子を見てみましょう:
母と子のお勉強 その2
母「今日から分数の約分っていうのをお勉強しようね。」
子「ふううん。約分ってなあに?」
母「うん。たとえば ![]() ていう分数があるわね。分母と分子を見てごらん?どちらも2で割り切れるでしょ。」
ていう分数があるわね。分母と分子を見てごらん?どちらも2で割り切れるでしょ。」
子「うん」
母「分母の4を2で割るといくら?」
子「えーと。4わる2は2だ。」
母「そうね。じゃあ、分子の2を2で割ると?2わる2はいくらかな?」
子「1だ」
母「そうね。このときね、分母と分子を線を引いてこう消して、今わった答をここに書くの。」
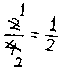
母「これが『約分』よ。書いてごらん。」(今、母が書いたのと同じことを書く。)
母「じゃ、次は、![]() を約分してみようか。」
を約分してみようか。」
母「分母も分子も同じ数で割れるわね。何で割れるかしら?」
子「うーーん。2かな?」
母「そうね。分母6わる2は、うん、割り切れるわね。あれ?分子はどう? 3わる2は…?」
子「あっ。 … 」
母「分子の3は何で割れる?」
子「えっと、3…、かな?」
母「そうね、そのとおり!分子の3は3で割り切れるわね。じゃあ、分母の6はどうかしら?同じ3でわれないかな?」
子「あ。われる、われる。 じゃ、両方とも3でわればいいんだ。」
母「そのとおり!よく見つけましたーー!! パチパチ」
母「じゃあ、書いてみようね。」(書いてみせる。)
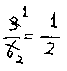
母「はい。同じように書いてごらん。」(今、母が書いたのと同じことを書く。)
母「よくできたわね。 ![]() を約分したら、答は
を約分したら、答は![]() でーす。約分って簡単でしょ。」
でーす。約分って簡単でしょ。」
子「ほんと、簡単だね。」
母「それじゃあ、いろんな分数の約分を練習しようね。 ![]() を約分するといくらになるかな?」
を約分するといくらになるかな?」
第1点めは、コラム01で指摘したのと同じ問題点です。
すなわち、上の指導だけでは、新しく出てきた「分数の約分」という概念の実体が体感できない、ということです。
上のお母さんの指導は、大変分かりやすい説明なので、子供は約分のやり方を正しく覚えていくでしょう。
けれども、この説明と練習を繰り返すだけでは、子供は「分数の約分」という概念の実体をつかめないのです。
![]() を約分して
を約分して![]() になるとは、いったいどういうことなのか?
になるとは、いったいどういうことなのか?
約分のやり方はわかったけれど、それっていったいどういうことなの? ということです。
小さい子供ほど、理由を気にせずに、吸収していきますから、上のように約分のやり方を説明するだけでも、十分に学習を進めていくことはできます。
しかし、数学的な力につなげていくためには、その概念にどのような実体があるのかを、あわせて教えてあげるのがベターです。
コラム01の解説で、ケーキやようかんを利用しました。
B1-1コースのあと、すぐにB1-2コース(約分)に入る場合は、スパイラルアップがスムーズに行われますから、改めてケーキなどを出してこなくても、大丈夫です。
図で説明してあげればいいのです。
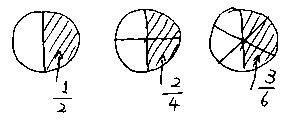
または、
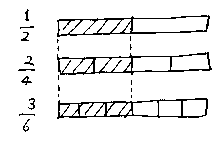
つまり、![]() も、
も、![]() も、その実体は、
も、その実体は、![]() と同じものなんだ、ということ。
と同じものなんだ、ということ。
図を見れば、すぐに分かりますね。
これは、実は、無数にある分数を「同値類」に整理してより単純な構造を把握するという、現代数学の常套手段と同じことをしているのです。
そこまで意識する必要はありませんが、教える側が、このような事も意識して教材を構成すると、子供は知らない間に、数学的考え方を身につけていくようになります。
ただし、実際に子供と面と向かって教えるときには、リズムが大切です。重点を置く場所を間違えると、子供のエネルギーはかえって停滞してしまいます。
説明がくどくならないようにしましょう。
上のお母さんの指導に、次のように付け加えるといいですね。
母「よくできたわね。 ![]() を約分したら、答は
を約分したら、答は![]() でーす。約分って簡単でしょ。」
でーす。約分って簡単でしょ。」
子「ほんと、簡単だね。」
母「![]() も
も![]() も、約分したら、どっちも同じ
も、約分したら、どっちも同じ![]() になるね。 ホラ。
になるね。 ホラ。
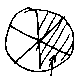 も、
も、 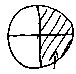 も、
も、 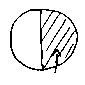 も
も
全部同じだね。」
子「ホントだー。」
ここには、大切な問題点が隠れています。
もう少し、母と子の勉強室の様子を見てみることにしましょう。
分母と分子の両方が同じ数で割り切れるんだけど、何で割ったらいいかしら?」
子「12 と 4 でしょ。うん。2だ!」
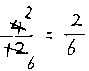
子供がこうするのはごく自然な流れです。そこで、
母「うん。よく分かったね。両方とも2で割り切れるね。ところで、2と6はどうかしら? まだ、同じ数で割り切れるんだけど、わかるかな?」
子どもは、このあたりでしんどくなってきます。エネルギーが急にガタンと落ちるかもしれません。
新しいことが次々と出て来すぎるからです。
![]() の約分を出した以上、ここで止めるわけには行きません。さらに、
の約分を出した以上、ここで止めるわけには行きません。さらに、
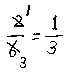
ここまでできることを押さえなければなりません。つまり、
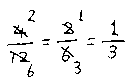
ですね。
実際には、分母と分子を4で約して、
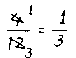
とやるのが効率的なわけです。
この練習も必要です。だから、お母さんが![]() の約分を練習用に用意していたことはいいことだったのです。
の約分を練習用に用意していたことはいいことだったのです。
ただし、約分の勉強に入ってまだ3問目です。これでは、早すぎます。
あまりにも急に新しいことを与えすぎると、子どもが、「せっかく約分ていうのができたと思ったのに、まだやらなきゃいけないの? あー。約分って大変」、こう感じてエネルギーを落としてしまうこともあります。そうなると、かんじんの約分の練習がしんどくなってしまいます。
無事越えていけるかもしれませんが、ここは、まだ何問かは、簡単なタイプの練習で「約分」を定着させたほうがいいでしょう。
実は、これがスムーズにできるように、現在の指導要領では、6年生になって「約数」や「倍数」の勉強をやったあと、やっと分数の約分に入るようになっているのです。
そこで、次のことを吟味しておく必要があります。すなわち、
約分を教える前に「最大公約数」を教えておく必要があるのではないか?
ということです。 同様に、
通分を教える前に「最小公倍数」を教えておく必要があるのではないか?
《スーパーらくらくスタディ》では、どうなっているのでしょう??
《スーパーらくらくスタディ》では、できるだけ予備知識は少なくて、学習を進めていけるように構成してあります。
「最大公約数」や「最小公倍数」は知らなくてかまいません。
「最大公約数」や「最小公倍数」を知らなくても、約分や通分は、スイスイできるようになります。
では、「最大公約数」というものを教えずに約分の指導をするのは、一体どうやったらいいのでしょう?
そこで使うのが、『バリエーショナル・エクササイズ』と『量質転化の法則』です。
上記のように、いきなり![]() の約分に入るのではなく、問題をきちんと精選して段階的に出してきます。
の約分に入るのではなく、問題をきちんと精選して段階的に出してきます。
![]() などと同じ程度に小さな数の分数で、もう少し、約分を練習させてあげるほうがいいでしょう。
などと同じ程度に小さな数の分数で、もう少し、約分を練習させてあげるほうがいいでしょう。
![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、…
、…
などの分数で、まずは、子供が分子と分母の両方を同時に割り切るような数を見つけて約分し、きちんと書くところまでを最初の目標とします。
ひとつひとつ、正しくできていたかどうかをフィードバックして子供に返してながら、練習を進めていきます。
子供が慣れないうちは、親が誘導してあげましょう。
そのとき、図を添えて約分の実体を、視覚的に見せてあげるようにしましょう。ひと目見せるだけで十分です。
約分する問題を何問か、そのようにしてやった段階で、次は図をつけずに、いきなり数字だけで処理するようにします。最初のバリエーションです。
そうして、ある程度「約分」というものに慣れてから、![]() のようなものを与えましょう。これが、第2のバリエーションです。
のようなものを与えましょう。これが、第2のバリエーションです。
当然子どもは2で約分して、「できた」と思っているでしょうから、
「ちょっと待って。もう、これ以上同じ数で割れないかな?」
と再び目を向けさせて、「もう1回、2で割れる」ことに着目させます。そして、初めに2で割るのではなくて一気に4で割れば速いことを体験させてあげればいいですね。
このあと、このような約分の練習を続けていきます。
このとき、いきなり何ででも約していくのではなく、「分母分子の両方を割り切るもっと大きな数はないかな?もうこれが一番大きい数かな?」と、一度立ち止まって考えさせるのです。
これが、とりもなおさず、最大公約数を探していることに他なりません。
この練習は、かなり数をこなして続けます。
こうして、この練習を数多く積み上げることによって、2つの数の最大公約数を求めることもサッとできるようになっていきます。
それはつまり、約分ができるようになるだけでなく、「最大公約数」の概念が、次第に把握されていくからです。
すなわち、練習の量をこなすことによって、「質」が深まっていくのです。
これが、『量質転化の法則』です。
十分この練習を積み上げた後、より大きな分母や分子を持つ分数の約分にレベルアップしていきます。
この段階(ステージ)を越えると、無作為にいろいろな分数を持ってきて約分したり、一つ一つではなく一気に5つ、さらには一気に10個の分数を約分したりするなど、『バリエーショナル・エクササイズ』はどんどん進めていくことができます。
市販の問題集なども、この段階まで来たら与えてあげるといいでしょう。
もうあとは、親が手を離していても、自分で問題集に取り組んでいくことができるのです。
こうしてみれば分かるように、「最大公約数」という用語は習わなくても、分数の約分を通して、「最大公約数」を体感的に理解していくことができるわけです。
※ ※ ※
今回の指導を考察してみましょう。
はじめのお母さんの指導は、《情知意サイクル》の《知》の部分に当たります。すばらしい教え方です。
ただ、《情》の部分が抜けていました。《情》すなわち「分数の約分の概念の実体」を体感させること。これを、問題点1の指摘によって補いました。
また、コース全体を通して、『バリエーショナル・エクササイズ』によって段階的にレベルアップしながら、練習量をこなして『量質転化の法則』につないでいきます。これを、問題点2の指摘によって補いました。
以上によって、B1-2コース(分数の約分)という一つのサイクルが完結します。
そしてそれは、更なる次のサイクルB1-3コース(分数の通分)へとスパイラルアップしていくのです。
. 《スーパーらくらくスタディ》は、このように構成されています。
子供たちが、らくらくとしかも確実に、分数を習得していくことができるという事実の奥には、このような緻密な分析と構成があるのです。
。。。。。。。。。。。。。。。。
。
。