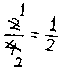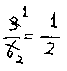|
T O
P | 基本理念 | コ
ラ ム
| 教 材
| Q & A
| お問い合わせ 算数・数学 02. 教え方 分数その2(分数の約分) 母と子の分数のお勉強、第2弾です。 |
|
||
|
母「今日から分数の約分っていうのをお勉強しようね。」 子「ふううん。約分ってなあに?」 母「うん。たとえば 子「うん」 母「分母の4を2で割るといくら?」 子「えーと。4わる2は2だ。」 母「そうね。じゃあ、分子の2を2で割ると?2わる2はいくらかな?」 子「1だ。」 母「そうね。このときね、分母と分子を線を引いてこう消して、今わった答をここに書くの。」 母「これが『約分』よ。書いてごらん。」(今、母が書いたのと同じことを書く。) 母「じゃ、次は、 母「分母も分子も同じ数で割れるわね。何で割れるかしら?」 子「うーーん。2かな?」 母「そうね。分母6わる2は、うん、割り切れるわね。あれ?分子はどう? 3わる2は…?」 子「あっ。 … 」 母「分子の3は何で割れる?」 子「えっと、3…、かな?」 母「そうね、そのとおり!分子の3は3で割り切れるわね。じゃあ、分母の6はどうかしら?同じ3でわれないかな?」 子「あ。われる、われる。 じゃ、両方とも3でわればいいんだ。」 母「そのとおり!よく見つけましたーー!! パチパチ」 母「じゃあ、書いてみようね。」(書いてみせる。) 母「はい。同じように書いてごらん。」(今、母が書いたのと同じことを書く。) 母「よくできたわね。 子「ほんと、簡単だね。」 母「それじゃあ、いろんな分数の約分を練習しようね。 お母さんは、このあと約分の練習を10問ほどやらせることができるように、初歩の問題集をかたわらに用意しています。 |
|||
|
今回も、お母さんは、段階的にとても上手に教えています。 まず、はじめに、 意気込んで「約分とは…」と厳密に全部教えてしまうのではなく、今までやってきた割り算から入っています。そして、約分の書き方までていねいに教えて、子供に書かせるところまでやっています。上手に誘導していますね。 そして、次に 今度は、はじめに「約分してみよう。」と言って、約分という言葉を使っています。こうすることで、いつの間にか子供は自然に約分の世界に入っています。 この指導がとてもすばらしいのは、 母が「分母も分子も同じ数で割れるわね。何で割れるかしら?」 と訊いて、子供が 「うーーん。2かな?」 と答えたときです。ほんとは2ではないんだけれど、子供と同じ目線に立って、 母「そうね。分母6わる2は、うん、割り切れるわね。」 と一度まず受け止めています。子供は、分母の6を見て、さっきと同じ2で割り切れると思ったのですね。その思いをまず受け止めてもらえた、ということが、子供の心を開放していきます。 このあとは、上のような誘導をしなくても、自分で「3だ」ということを見つけていくこともよくあります。そして、上の指導においても、子供は「3」という数を自分で見つけたという感触を持てるでしょう。 さあ。ここまで、 母「それじゃあ、いろんな分数の約分を練習しようね。 と、次の段階へつないでいます。 お母さんは、このあと、初歩の問題集で、約分の練習を10問ほどやらせることができるかな、と考えています。 このように、少しずつレベルを上げながら、「約分」に慣らしていく配慮もすばらしいです。 さて、それでは、この指導における問題点は何でしょうか? この問題点を認識することなく、指導を進めていっても、子供はそれなりに約分をできるようになっていきはするでしょう。 けれども、このような一つの勉強を通して数学的な力を育むためには、その認識があるのとないのとでは、大きな違いが出てきます。 そのような認識を得るためには、原理や法則を知ることが大切です。 『秘法 スーパーらくらくスタディ 直伝編』に、それらを解説してあります。 ここでは、《情知意サイクル》の「情」と「知」に関する理解が大切です。さらに、《バリエーショナル・エクササイズ》と《量質転化の法則》を理解することで、子供の力は飛躍的についていきます。 このあとは、専用コラムをご覧ください。
|